Complex-valued Signal Processing

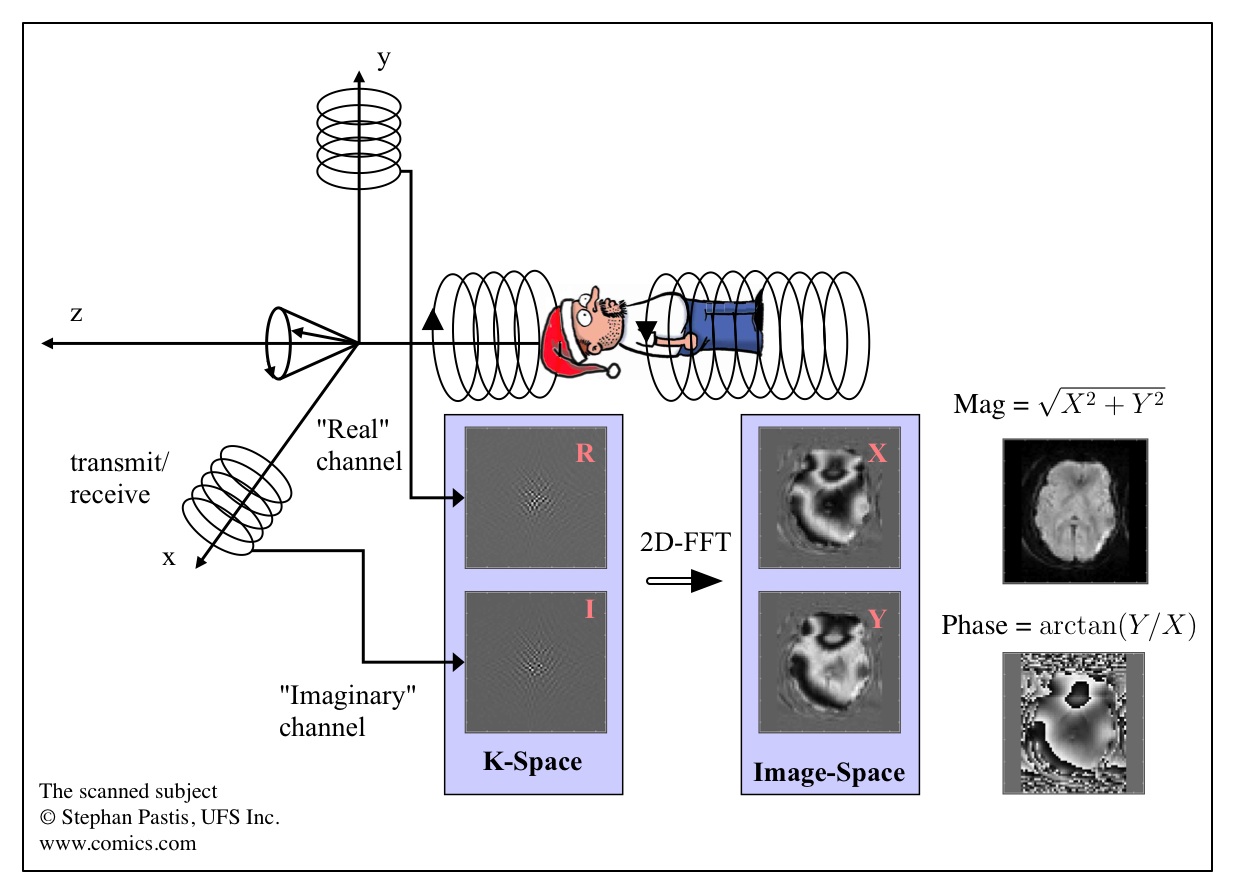GIFT Complex-valued signals arise frequently in applications as diverse as communications, radar, and biomedicine, as most practical modulation formats are of complex type and applications such as radar and magnetic resonance imaging lead to data that are inherently complex valued. Processing in the complex domain presents a number of challenges, and as a result, the vast majority of algorithms developed for the complex domain have taken shortcuts limiting their usefulness. Our group works on developing algorithms for complex-valued signal processing such that the full potential of complex-valued signal processing can be realized and many simplifying assumptions can be eliminated.

Key references:

  • T. Adali and P. J. Schreier, "Optimization and estimation of complex-valued signals: Theory and applications in filtering and blind source separation," IEEE Signal Processing Magazine, to appear, Sep. 2014.
    omplex-valued signals occur in many areas of science and engineering and are thus of fundamental interest. When developing signal processing methods in the complex domain, there are two key issues: making use of the full statistical information and optimization. In this article, we review the necessary tools to address these two key issues and provide examples in filtering and blind source separation (BSS) that utilize these tools.

  • T. Adali, P. J. Schreier, and L. L. Scharf, "Complex-valued signal processing: The proper way to deal with impropriety," IEEE Trans. Signal Processing, vol. 59, no. 11, pp. 5101-5123, Nov. 2011 (Top 100 most downloaded IEEE Xplore article for the period July 2011--Dec. 2011).
    This is an overview article on optimization in the complex domain using Wirtinger calculus and on full characterization of complex-valued statistics. The article also addresses the question on how to decide when to take noncircularity into account, noncircularity detection, widely linear filtering, and independent component analysis in the complex domain.

  • T. Adali, H. Li, M. Novey, and J.-F. Cardoso, "Complex ICA using nonlinear functions," IEEE Trans. Signal Processing, vol. 56, no. 9, pp. 4536--4544, Sept. 2008 (2010 IEEE Signal Processing Society Best Paper Award).
    • We introduce a framework based on Wirtinger calculus for nonlinear complex-valued signal processing such that all computations can be directly carried out in the complex domain. The two main approaches for performing independent component analysis, maximum likelihood and maximization of non-Gaussianity--which are intimately related to each other--are studied using this framework. The main update rules for the two approaches are derived, their properties and density matching strategies are discussed along with numerical examples to highlight their relationships.

Recent related projects:

    Collaborative Research: Complex-Valued Signal Processing and its Application to Analysis of Brain Imaging Data
    Funded by NSF-CCF (Award no: 0635129) and Complex-Valued Signal Processing and its Application to Analysis of Brain Imaging Data Funded by NSF-CCF (Award no: 0840895 -- additional funding)
    We establish a framework for complex-valued signal processing such that all computations can be carried out in the complex domain eliminating the need for many simplifying assumptions, such as the circularity of signal, both in the derivation and the analysis of the algorithms. We demonstrate the application of the framework for deriving a new class of efficient algorithms for performing complex ICA, and in particular, for studying brain function using the medical imaging data in its native, complex form.

    Collaborative Research: SEI: Independent Component Analysis of Complex-Valued Brain Imaging Data
    Funded by NSF-IIS (Award nos: 0612076 and 0715022 (0612104))
    We develop a class of complex ICA algorithms, in particular for analysis of biomedical imaging data and demonstrate the power of joint data analysis as well as performing the analysis on the complete set of data, i.e., by utilizing both the magnitude and the phase information. We focus upon three image types, functional magnetic resonance imaging (fMRI), structural MRI (sMRI) and diffusion tensor imaging (DTI). These three imaging data provide complementary information about brain connectivity, and all can benefit from the incorporation of a complex-valued data processing approach.

Selected other publications:

  • T. Kim and T. Adali, "Approximation by fully-complex multilayer perceptrons," Neural Computation, vol. 15, no. 7, pp. 1641-1666, July 2003.
    • We extend the result on the approximation ability of the multilayer perceptron to the complex domain by classifying nonlinear functions based on their singularities. The approximation theorems for the first two classes of elementary transcendental functions are very general and resemble the universal approximation theorem for the real-valued feedforward multilayer perceptron that was shown almost concurrently by multiple authors in 1989 (Cybenko, 1989; Hornik and Stinchecombe, and White, 1989; Funahashi, 1989). The third approximation theorem for the complex multilayer perceptron is unique and related to the power series approximation that can represent any complex number arbitrarily closely in the deleted neighborhood of a singularity.
  • J.-F. Cardoso and T. Adali, “ The maximum likelihood approach to complex ICA,” in Proc. IEEE Int. Conf. Acoust., Speech, Signal Processing (ICASSP), Toulouse, France, May 2006.
    • We derive the form of the best non-linear functions for performing independent component analysis by maximum likelihood estimation and discuss several special cases for the score function as well as adaptive scores.

Project team:

    Current: Geng-Shen Fu, Rami Mowakeaa, Dr. Matthew Anderson, and Dr. Tülay Adali
    Others: Dr. Mike Novey, Dr. Xi-Lin Li, Dr. Hualiang Li, Josselin Dea, and Dr. Taehwan Kim

Resources:

  • Actual complex fMRI dataset: We have used a complex fMRI dataset containing data from 16 subjects performing a finger tapping task in W. Xiong, Y.-O. Li, H. Li, T. Adali, and V. D. Calhoun, "On ICA of complex-valued fMRI: Advantages and order selection," in Proc. IEEE Int. Conf. Acoust., Speech, Signal Processing (ICASSP), Las Vegas, Nevada, April 2008. To request this complex-valued fMRI dataset, please send an email to Dr. Adali (adali AT umbc.edu).