Subspace partitioning algorithm

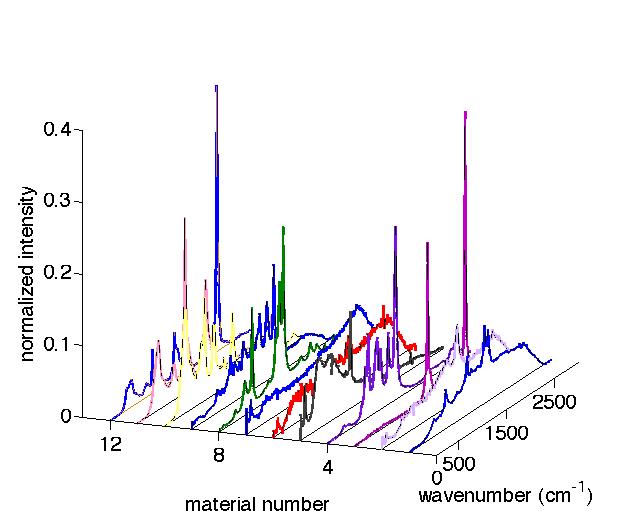
The subspace partitioning algorithm is applied to the chemical detection problem in Raman spectroscopy. Some sample Raman spectra are shown in Fig. 1. The library in the package includes Raman spectra of 30 toxic chemicals and 19 background materials*.


Raman library Spectra

The library paritioning algorithm proceeds as follows [1]:

  • 1. Find forbidden pairs in the library.
  • 2. Use graph coloring algorithm to partition thelibrary.
  • 3. Form spectrum clusters for future detection.

    • After partitioning, chemicals are assigned into 4 clusters:

    cluster # spectrum index in each cluster
    c1 7 8 12 17 18 20 23 29
    c2 3 5 13 14 16 21 24
    c3 1 4 11 15 19 22 25
    c4 2 6 9 10 27 28 30

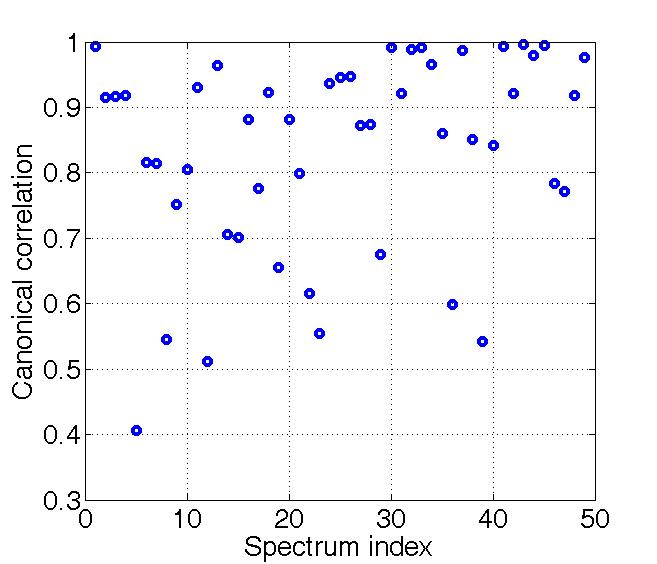
    BeforePartitioning

    Fig. 2 shows the intra-library canonical correlations of each spectrum before partitioning. Some correlation values are very close to one, which implies an ill-conditioned subspace.


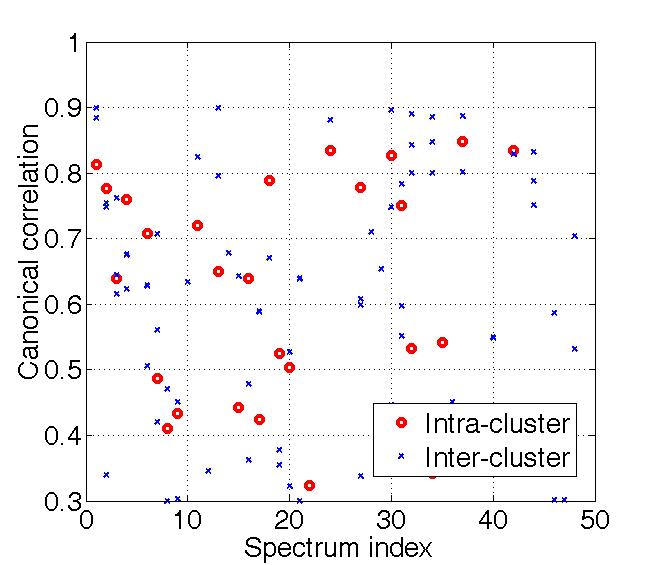
    AfterPartitioning

    Fig. 3 show both the intra- and inter-cluster canonical correlations for each spectrum in the library after partitioning. We can see that all the correlation values are below a given threshold 0.9.

    References:

    [1] W. Wang, T. Adali and D. Emge, "Subspace partitioning for target detection and identification," IEEE Trans. on Signal Processing, vol. 57, no. 4, Apr. 2009.

    Downloads:

      The subspace partitioning algorithm is implemented in Matlab. The package can be downloaded from link: Subspace partitioning code, Main script: TSP08_LibraryPartitioning_main.m.
      Questions can be sent to: wangw1@umbc.edu or adali@umbc.edu

    *The Raman library in this package is a reduced library compared to the one used in [1] due to the security reason.