M-CCA algorithm

There are five cost functions used for M-CCA algorithm development [1], MAXVAR, MINVAR, SUMCOR, SSQCOR, and GENVAR. Among these cost functions, MAXVAR and MINVAR lead to direct solutions. M-CCA algorithm based on the other three cost functions, SUMCOR, SSQCOR, and GENVAR utilizes iterative procedures to optimize the cost and hence the initial condition has an impact on the solution.

Test of robustness: to test the robustness of iterative M-CCA algorithms, we generate simulated group datasets and apply M-CCA algorithm based on SSQCOR. We perform multiple Monte Carlo trials of the algorithm on the same simulated datasets. In each trial, a random initialization is given to the demixing vectors to start the iterative optimization of the cost function. We collect the estimated demixing vectors and calculate the Euclidean distance among the estimated demixing vectors for each source at different trials.

As an example,  the correlation matrix of a group of simulated sources is shown in Figure 1.

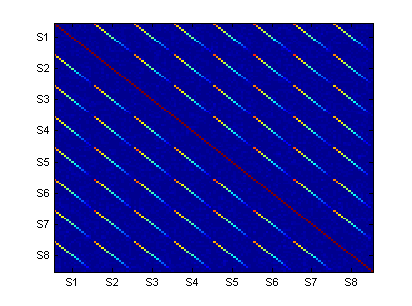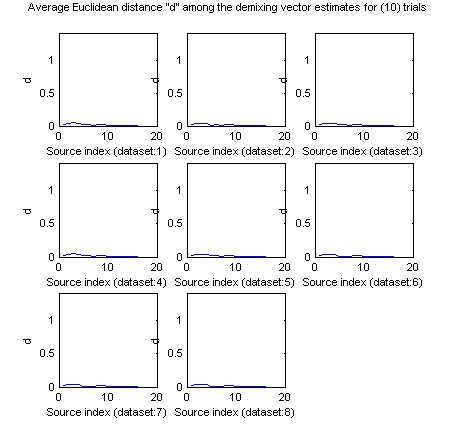Figure 1 Correlation matrix of the simulated sources (8 datasets x 16 sources per dataset)

A sample output of robustness test results is shown in Figure 2.

Figure 2 Sample output of the robustness test script (8 datasets x 16 sources per dataset, 20 Mont Carlo trials)

References:

[1] J. R. Kettenring, Canonical analysis of several sets of variables, Biometrika, vol. 58, pp. 433-51, 1971.

[2] Y.-O. Li, W. Wang, T. Adali, and V. D. Calhoun, "CCA for joint blind source separation of multiple datasets with application to group fMRI analysis," in Proc. IEEE International Conference on Acoustics, Speech, and Signal Processing (ICASSP 2008), Las Vegas, NV.

Downloads:

    For implementation and robustness test of M-CCA, download the package from link: Matlab script, unzip the package to form a working directory.
    Main script: exp_cca_multiset_bss_robustness_public.m;
    Subfunctions: rand_laplacian.m, ssq_cca_efficient.m;
    Questions can be sent to: liyiou1 (at) umbc (dot) edu